证明过程#
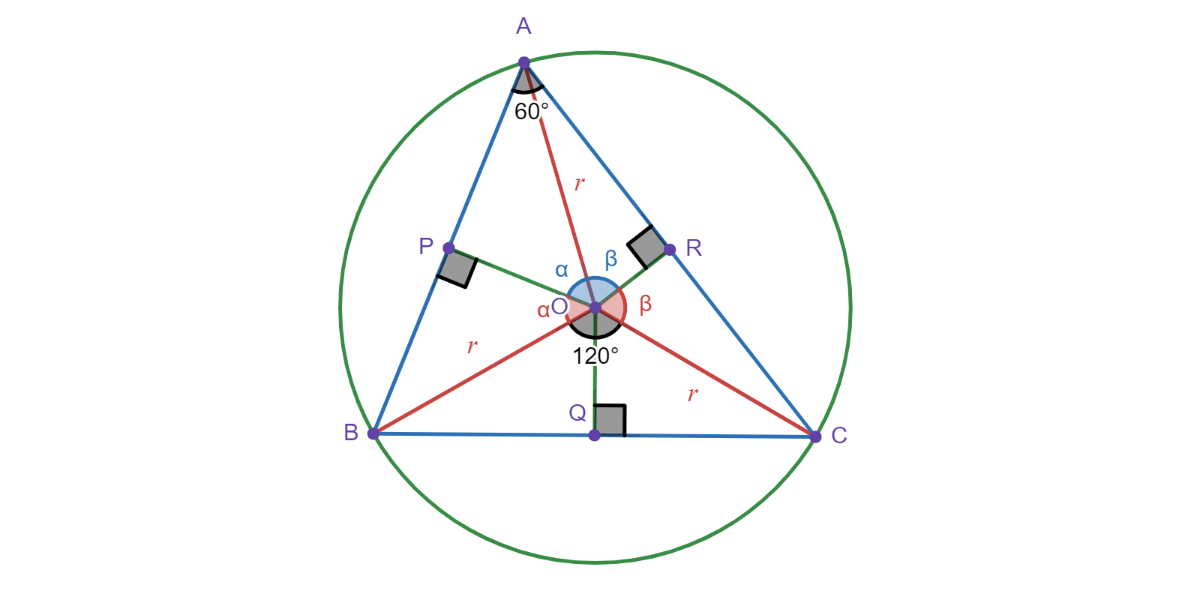
设⊙O的半径长为r,∠AOB=2α,∠AOC=2β
在⊙O中,∵∠A=60°
∴∠BOC=2∠A=120°
∵OB=OC,OQ⊥BC
∴∠BOQ=21∠BOC=60°,BC=2BQ
∴BC=2BQ=2(OB⋅sin60°)=2(r⋅23)=3r
同理AB=2r⋅sinα,AC=2r⋅sinβ
∵∠AOB+∠AOC+∠BOC=360°
即2α+2β+120°=360°
∴α+β=120°
则AB+AC=2r⋅(sinα+sin(120°−α))=23r⋅sin(α+30°)
令AB+AC=2BC,即23r⋅sin(α+30°)=23r
又∵α>0°,∴解得α=60°
此时∠AOB=∠AOC=120°即△ABC为等边三角形
∴仅当△为等边三角形时,才满足AB+AC=2BC
∴原命题得证