现在中考数学越来越爱考反演变换的题目了,于是……就有了这篇文章。
{% note yellow fa-siren-on %}
本篇章阅读需要前置知识:圆幂定理 ,建议先阅读此篇章再回来,如已掌握请忽略。
{% endnote %}
反演变换与平移、旋转、对称变换等类似,也属于一种几何变换,但它更像是作一个图形关于圆的镜像。简单来讲,其定义如下:在同一平面内,有共线的三点 A , O , A ′ A,O,A' A , O , A ′ O O O O A ⋅ O A ′ = k OA\cdot OA'=k O A ⋅ O A ′ = k k k k A A A A ′ A' A ′ ,记作 I ( O , k ) I(O,k) I ( O , k ) O O O 反演中心**,常数 k k k 反演幂 ,点 A ′ A' A ′ A A A 反点 。对于反演变换 I ( O , k ) I(O,k) I ( O , k ) r = k r=\sqrt{k} r = k O O O r r r I ( O , k ) I(O,k) I ( O , k ) 反演圆 或基圆 ,常数 r r r 反演半径 。如下图所示。
反演变换的性质有很多条,由于篇幅有限,而且出于入门目的,这里仅简单列举两条易懂且常用的性质。
性质 1:反演变换可逆# 由反演变换的定义可知,当 A ′ A' A ′ A A A A A A A ′ A' A ′ A A A A ′ A' A ′
性质 2:(每个点经过反演变换前后的位置关系)#
位于反演圆上 的点,其反点保持在原处 。
位于反演圆内 的点,其反点位于反演圆外 。
位于反演圆外 的点,其反点位于反演圆内 。
了解完反演变换的两条基本性质,那么就进入正题:反演变换在初中数学中的应用。
初中数学的反演变换通常会出现在求解动点轨迹 的一类问题中,尤其是双动点问题 (含一主动点和一从动点),当然部分求最值问题的本质也是求出动点轨迹 。
根据反演变换的定义 瓜豆原理 的“定比定角”。以下会举一个简单的例子进行说明。
平面内有一定点 O O O P , Q P,Q P , Q Q Q Q P P P P P P O P ⋅ O Q = k OP\cdot OQ=k OP ⋅ OQ = k ∠ P O Q = θ \angle POQ=\theta ∠ POQ = θ k k k θ \theta θ Q Q Q
第Ⅰ类#
点 P P P O O O 线生线 )
显然,由于此时 ∠ P O Q \angle POQ ∠ POQ O P OP OP O Q OQ OQ Q Q Q 过点 O O O )上运动。动图如下。
这一类即所谓线生线 。
第Ⅱ类#
点 P P P 不经过 O O O 线生圆 )
肉眼可见地,这一类与上一类有了天差地别,点 Q Q Q
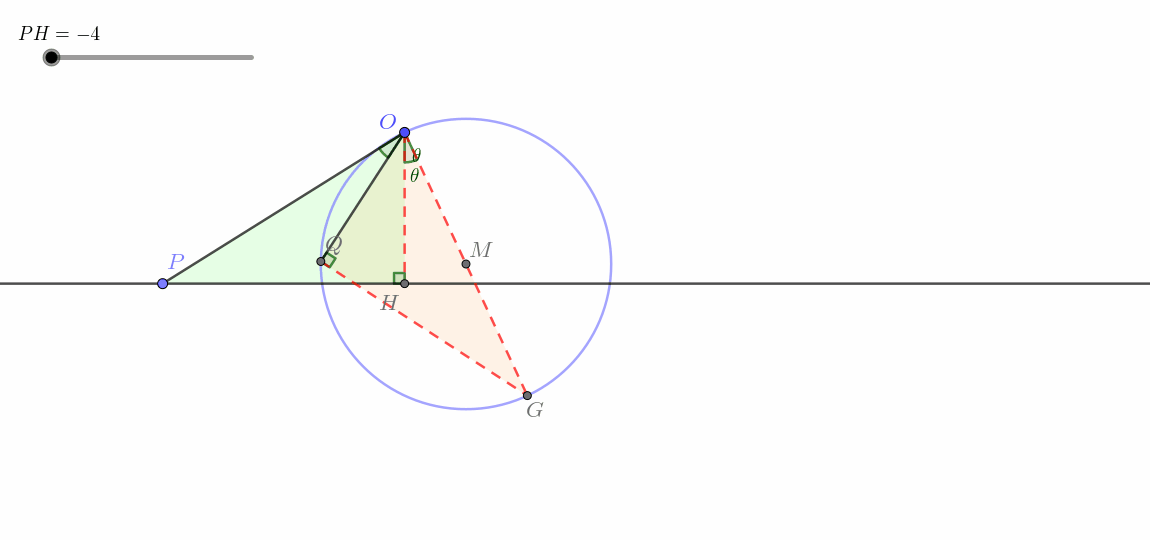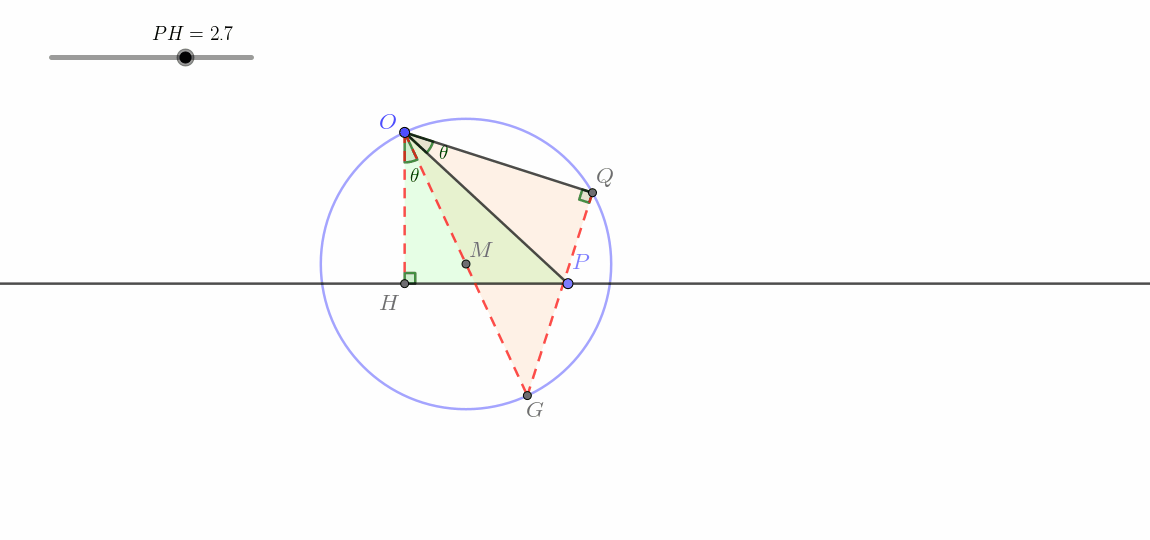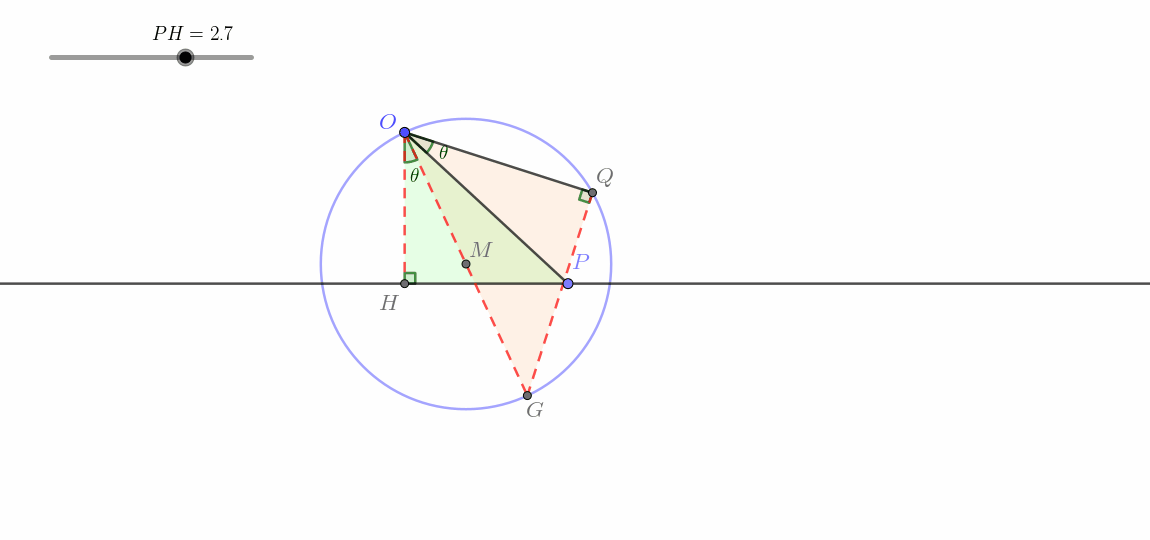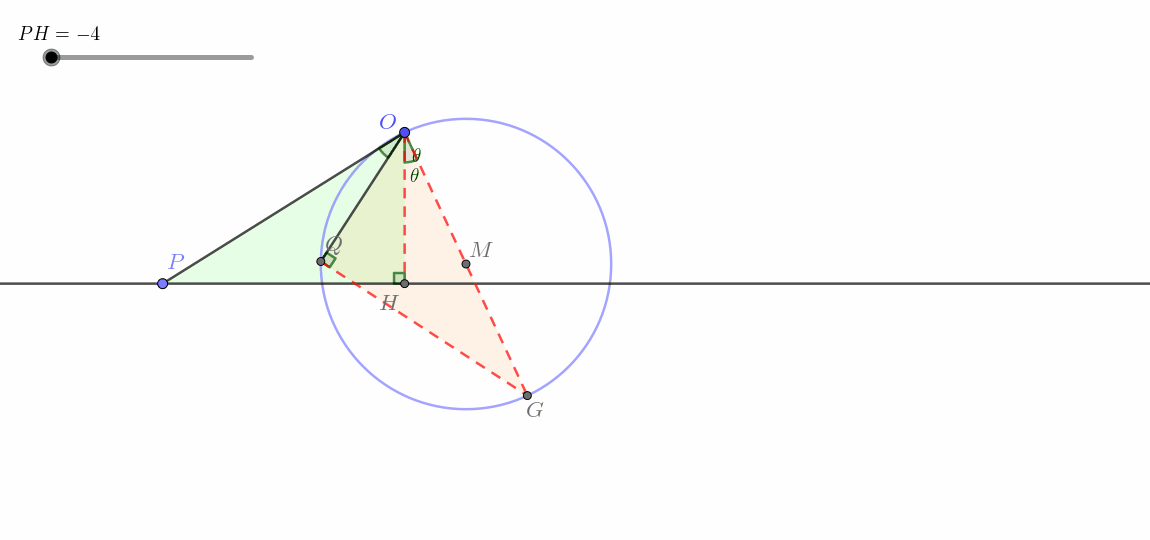
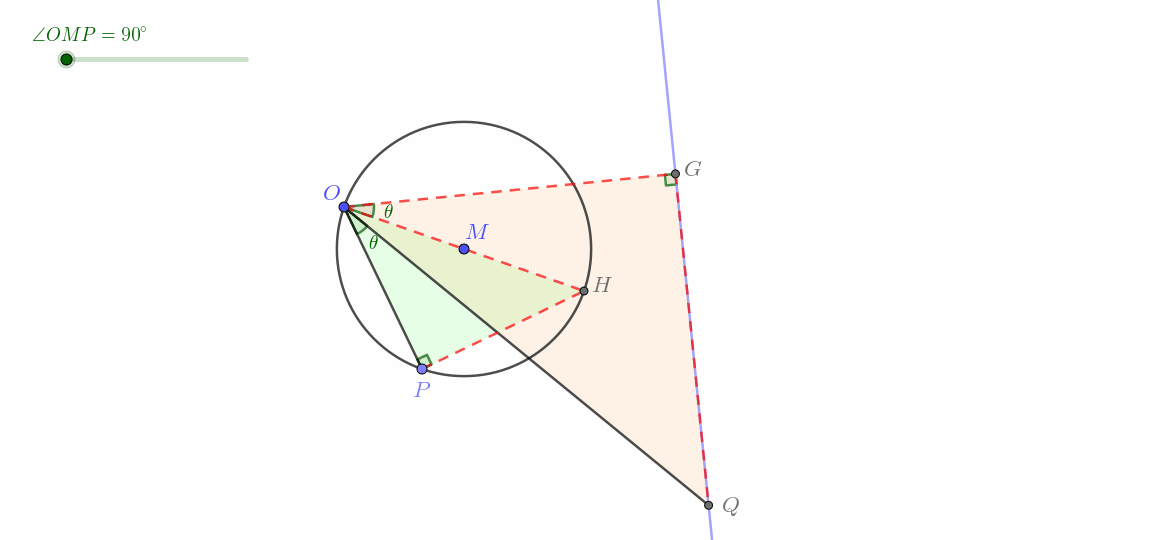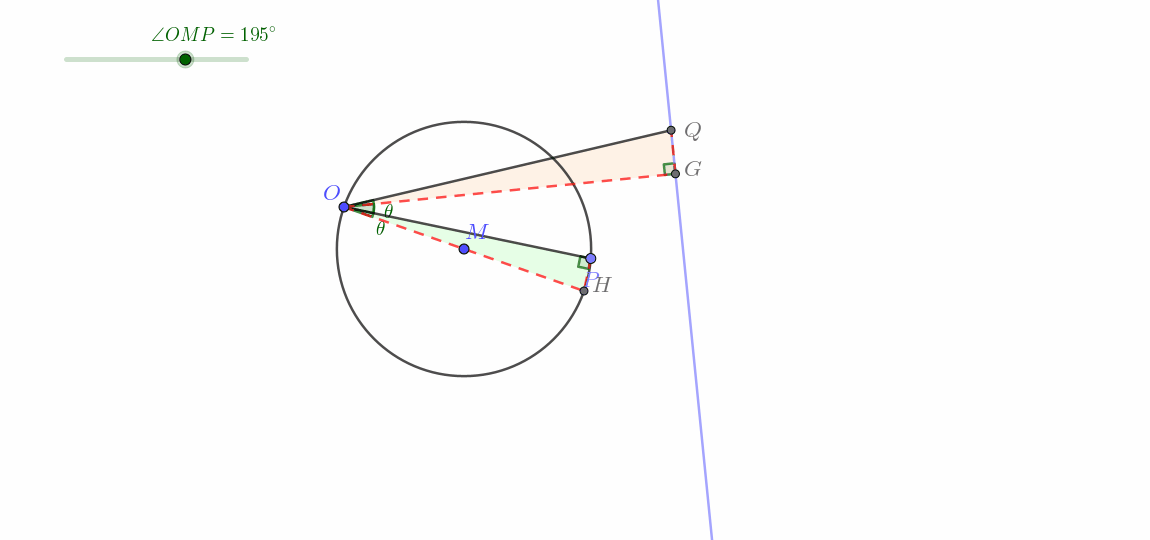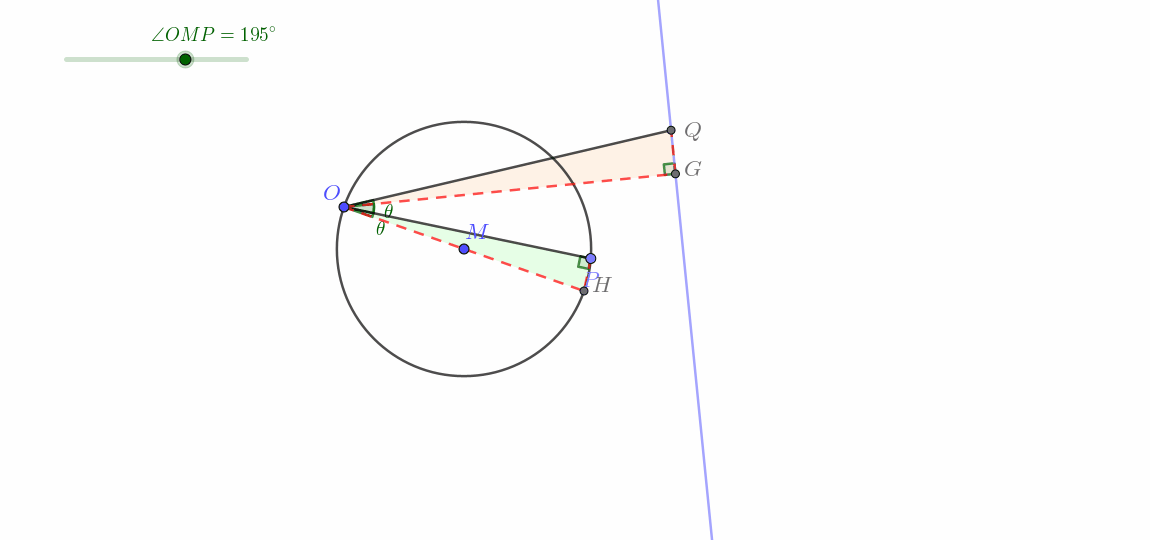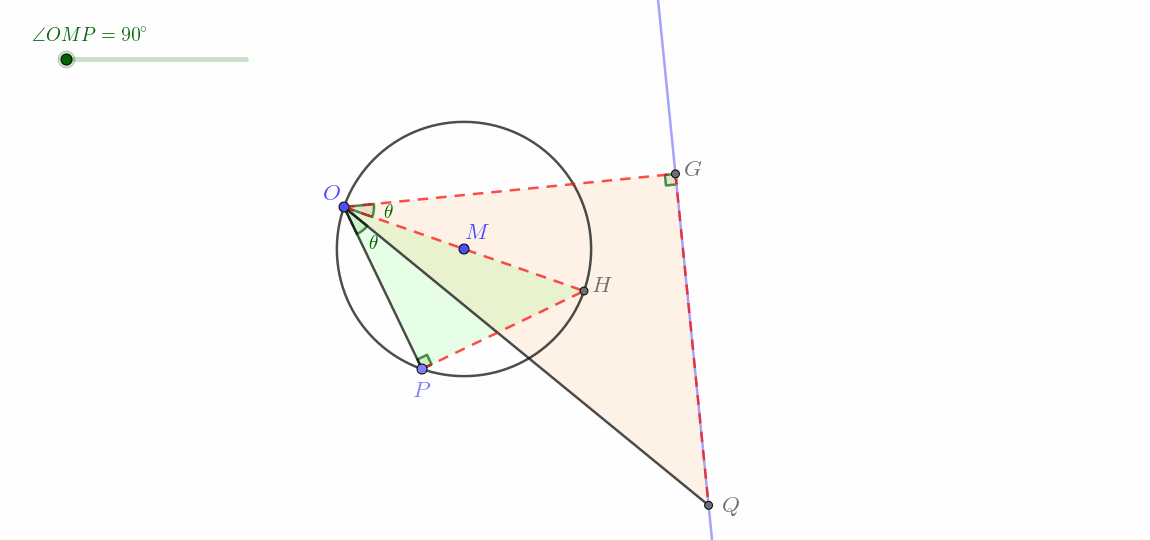
过点 O 作 O H ⊥ H P 于点 H ,在平面内取一点 G ,使得 ∠ H O G = ∠ P O Q ,且 ∠ O Q G = 90 ° ,连接 O G , Q G ,取 O G 中点 M . ∵ ∠ H O G = ∠ P O Q ∴ ∠ H O G + ∠ P O G = ∠ P O Q + ∠ P O G 即 ∠ P O H = ∠ G O Q ∵ O H ⊥ H P ∴ ∠ P H O = 90 ° = ∠ G Q O ∴ △ P O H ∽ △ G O Q ∴ O P O G = O H O Q 即 O H ⋅ O G = O P ⋅ O Q = k ∵ O H 为定值, k 为常数 ∴ O G 为定值 又 ∵ ∠ H O G = ∠ P O Q 为定值, O H 固定 ∴ O G 固定 ∵ ∠ O Q G = 90 ° 为定角 ∴ 点 Q 在以 O G 为直径的圆上运动 即点 Q 在以 M 为圆心, O M 为半径的圆上运动(过点 O 的圆) \begin{align}
&过点O作OH\perp HP于点H,在平面内取一点G,使得\angle HOG=\angle POQ,且\angle OQG=90\degree,连接OG,QG,取OG中点M.\\
&\because \angle HOG=\angle POQ\\
&\therefore \angle HOG+\angle POG=\angle POQ+\angle POG\\
&即\angle POH=\angle GOQ\\
&\because OH\perp HP\\
&\therefore \angle PHO=90\degree=\angle GQO\\
&\therefore \triangle POH\backsim \triangle GOQ\\
&\therefore \frac{OP}{OG}=\frac{OH}{OQ}\\
&即OH\cdot OG=OP\cdot OQ=k\\
&\because OH为定值,k为常数\\
&\therefore OG为定值\\
&又\because \angle HOG=\angle POQ为定值,OH固定\\
&\therefore OG固定\\
&\because \angle OQG=90\degree 为定角\\
&\therefore 点Q在以OG为直径的圆上运动\\
&\color{red}{\boldsymbol{即点Q在以M为圆心,OM为半径的圆上运动(过点O的圆)}}\\
\end{align} 过点 O 作 O H ⊥ H P 于点 H ,在平面内取一点 G ,使得 ∠ H OG = ∠ POQ ,且 ∠ OQG = 90° ,连接 OG , QG ,取 OG 中点 M . ∵ ∠ H OG = ∠ POQ ∴ ∠ H OG + ∠ POG = ∠ POQ + ∠ POG 即 ∠ PO H = ∠ GOQ ∵ O H ⊥ H P ∴ ∠ P H O = 90° = ∠ GQO ∴ △ PO H ∽ △ GOQ ∴ OG OP = OQ O H 即 O H ⋅ OG = OP ⋅ OQ = k ∵ O H 为定值, k 为常数 ∴ OG 为定值 又 ∵ ∠ H OG = ∠ POQ 为定值, O H 固定 ∴ OG 固定 ∵ ∠ OQG = 90° 为定角 ∴ 点 Q 在以 OG 为直径的圆上运动 即点 Q 在以 M 为圆心, OM 为半径的圆上运动(过点 O 的圆) 动图如下。
这一类即所谓线生圆 。
第Ⅲ类#
点 P P P O O O M M M 圆生线 )
这一类与第Ⅱ类十分类似,只是调换了以下顺序,所以其实时可以直接利用反演变换的性质1
连接 O M 并延长交 ⊙ M 于点 H ,连接 P H ,在平面内取一点 G ,使得 ∠ H O G = ∠ P O Q ,且 ∠ O G Q = 90 ° ,连接 O G , Q G . 由题,知 O H 为直径 ∴ ∠ O P H = 90 ° = ∠ O G Q ∵ ∠ H O G = ∠ P O Q ∴ H O G − ∠ H O Q = ∠ P O Q − ∠ H O Q 即 ∠ G O Q = ∠ P O H 又 ∵ ∠ O P H = ∠ O G Q ∴ △ P O H ∽ △ G O Q ∴ O P O G = O H O Q 即 O H ⋅ O G = O P ⋅ O Q = k ∵ O H 为定值, k 为常数 ∴ O G 为定值 又 ∵ ∠ H O G = ∠ P O Q 为定值, O H 固定 ∴ O G 固定 ∵ ∠ O G Q = 90 ° 为定角 ∴ 点 Q 在过点 G 且垂直于 O G 的直线上运动 即点 Q 在如图所示的蓝色直线上运动(不经过点 O 的直线) \begin{align}
&连接OM并延长交\odot M于点H,连接PH,在平面内取一点G,使得\angle HOG=\angle POQ,且\angle OGQ=90\degree,连接OG,QG.\\
&由题,知OH为直径\\
&\therefore\angle OPH=90\degree=\angle OGQ\\
&\because\angle HOG=\angle POQ\\
&\therefore HOG-\angle HOQ=\angle POQ-\angle HOQ\\
&即\angle GOQ=\angle POH\\
&又\because\angle OPH=\angle OGQ\\
&\therefore\triangle POH\backsim\triangle GOQ\\
&\therefore\frac{OP}{OG}=\frac{OH}{OQ}\\
&即OH\cdot OG=OP\cdot OQ=k\\
&\because OH为定值,k为常数\\
&\therefore OG为定值\\
&又\because\angle HOG=\angle POQ为定值,OH固定\\
&\therefore OG固定\\
&\because \angle OGQ=90\degree 为定角\\
&\therefore 点Q在过点G且垂直于OG的直线上运动\\
&\color{red}{\boldsymbol{即点Q在如图所示的蓝色直线上运动(不经过点O的直线)}}\\
\end{align} 连接 OM 并延长交 ⊙ M 于点 H ,连接 P H ,在平面内取一点 G ,使得 ∠ H OG = ∠ POQ ,且 ∠ OGQ = 90° ,连接 OG , QG . 由题,知 O H 为直径 ∴ ∠ OP H = 90° = ∠ OGQ ∵ ∠ H OG = ∠ POQ ∴ H OG − ∠ H OQ = ∠ POQ − ∠ H OQ 即 ∠ GOQ = ∠ PO H 又 ∵ ∠ OP H = ∠ OGQ ∴ △ PO H ∽ △ GOQ ∴ OG OP = OQ O H 即 O H ⋅ OG = OP ⋅ OQ = k ∵ O H 为定值, k 为常数 ∴ OG 为定值 又 ∵ ∠ H OG = ∠ POQ 为定值, O H 固定 ∴ OG 固定 ∵ ∠ OGQ = 90° 为定角 ∴ 点 Q 在过点 G 且垂直于 OG 的直线上运动 即点 Q 在如图所示的蓝色直线上运动(不经过点 O 的直线) 动图如下。
这一类即所谓圆生线 。
第Ⅳ类#
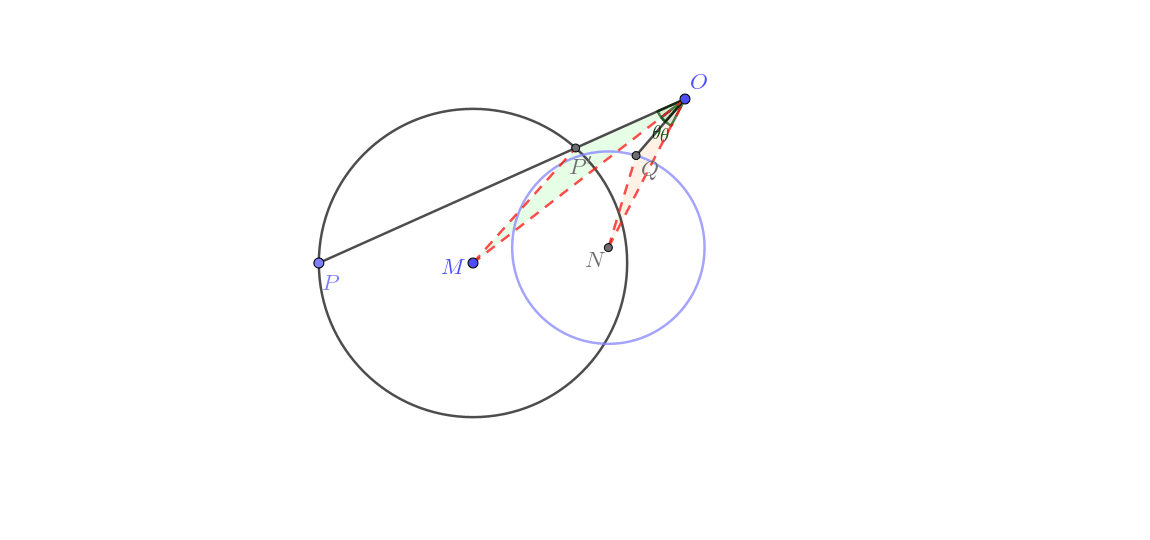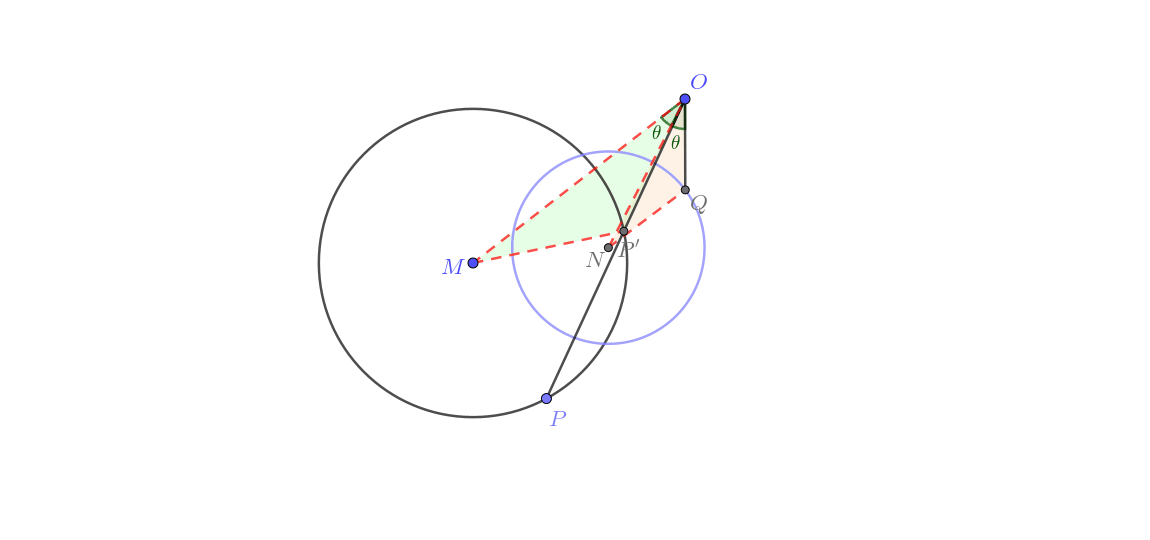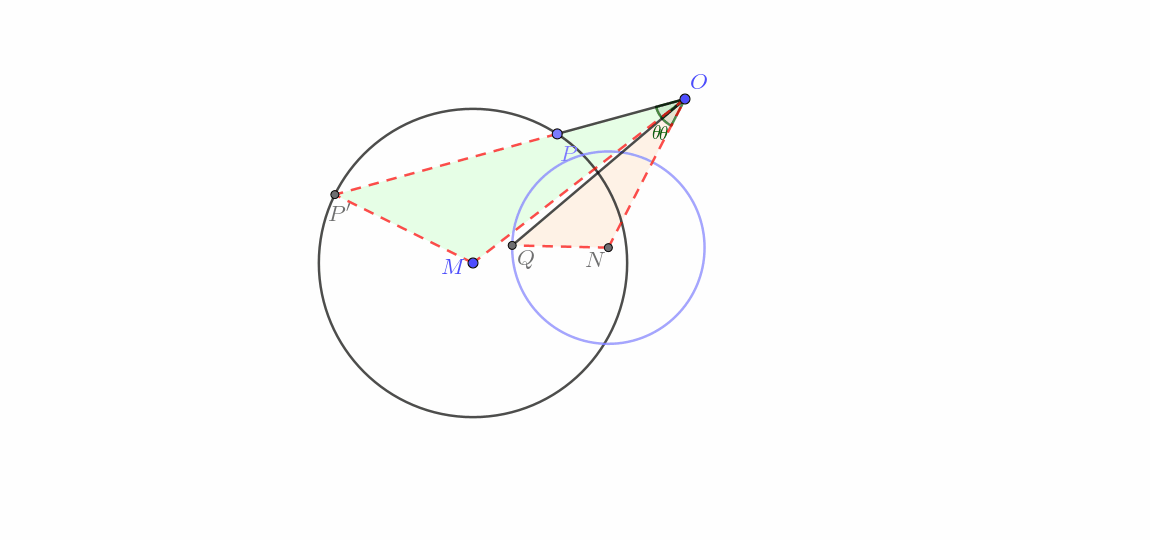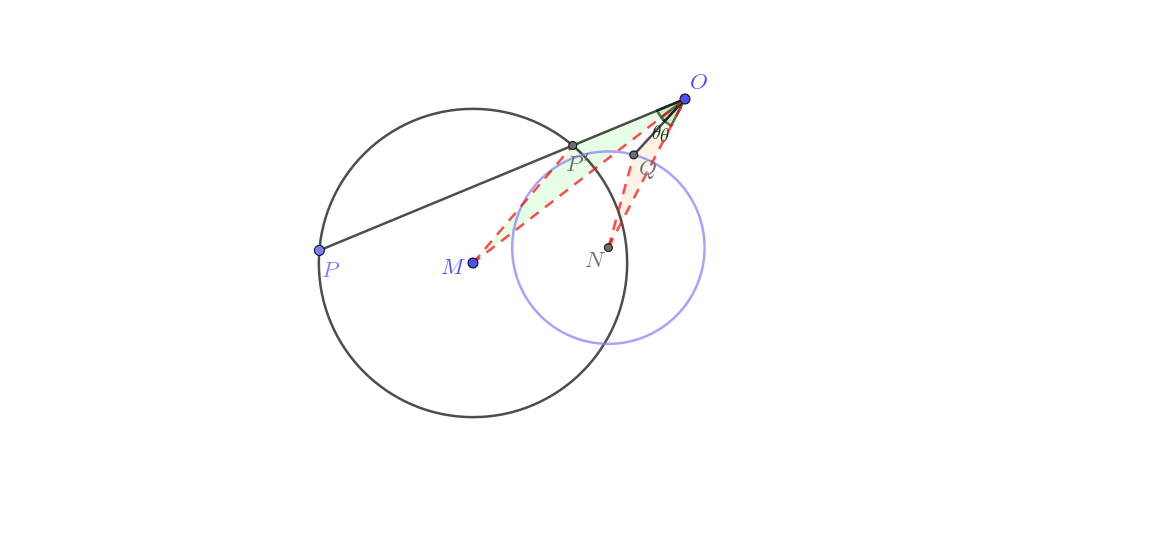
点 P P P 不经过 O O O M M M 圆生圆 )
由图可知这一类的做法与前三组更是又显著差异。其实这里用到了“转化 ”的主要思想,通过将反演问题由圆幂定理 进行转化,把题目变为简单的“瓜豆” 题。其大致证明如下。
阅读此证明需要知识【圆幂定理】,点我跳转 ,如已掌握请忽略。
连接 O M ,连接 O P 并延长交 ⊙ M 与点 P ′ ,连接 M P ′ ,在平面内取一点 N ,使得 ∠ M O N = ∠ P O Q , ∠ O Q N = ∠ O P ′ M ,连接 O N , Q N . ∵ ∠ M O N = ∠ P O Q ∴ ∠ M O N − ∠ P ′ O N = ∠ P O Q − ∠ P ′ O N 即 ∠ M O P ′ = ∠ N O Q 又 ∵ ∠ O Q N = ∠ O P ′ M ∴ △ M O P ′ ∽ △ N O Q ∴ O M O N = M P ′ N Q = O P ′ O Q 在 ⊙ M 中,记其半径为 r ,则根据圆幂定理 得 O P ⋅ O P ′ = O M 2 − r 2 ,记为 a 又 O P ⋅ O Q = k ,记为 b ∴ a b ,得 O P ′ O Q = O M 2 − r 2 k ∵ O M , r , k 都为定值 ∴ O P ′ O Q 为定值 ∵ O M O N = M P ′ N Q = O P ′ O Q 又 ∵ O M , M P ′ 为定值 ∴ O N , N Q 为定值 又 ∵ O M 固定, ∠ M O N = ∠ P O Q 为定值 ∴ O N 固定 ∴ 点 Q 在以 N 为圆心, N Q 为半径的圆上运动(不经过点 O 的圆) \begin{align}
&连接OM,连接OP并延长交\odot M与点P',连接MP',在平面内取一点N,使得\angle MON=\angle POQ,\angle OQN=\angle OP'M,连接ON,QN.\\
&\because\angle MON=\angle POQ\\
&\therefore\angle MON-\angle P'ON=\angle POQ-\angle P'ON\\
&即\angle MOP'=\angle NOQ\\
&又\because\angle OQN=\angle OP'M\\
&\therefore\triangle MOP'\backsim\triangle NOQ\\
&\therefore\frac{OM}{ON}=\frac{MP'}{NQ}=\frac{OP'}{OQ}\\
&在\odot M中,记其半径为r,则根据圆幂定理\\
&得OP\cdot OP'=OM^2-r^2,记为a\\
&又OP\cdot OQ=k,记为b\\
&\therefore\frac{a}{b},得\frac{OP'}{OQ}=\frac{OM^2-r^2}{k}\\
&\because OM,r,k都为定值\\
&\therefore \frac{OP'}{OQ}为定值\\
&\because\frac{OM}{ON}=\frac{MP'}{NQ}=\frac{OP'}{OQ}\\
&又\because OM,MP'为定值\\
&\therefore ON,NQ为定值\\
&又\because OM固定,\angle MON=\angle POQ为定值\\
&\therefore ON固定\\
&\color{red}{\boldsymbol{\therefore 点Q在以N为圆心,NQ为半径的圆上运动(不经过点O的圆)}}\\
\end{align} 连接 OM ,连接 OP 并延长交 ⊙ M 与点 P ′ ,连接 M P ′ ,在平面内取一点 N ,使得 ∠ MON = ∠ POQ , ∠ OQN = ∠ O P ′ M ,连接 ON , QN . ∵ ∠ MON = ∠ POQ ∴ ∠ MON − ∠ P ′ ON = ∠ POQ − ∠ P ′ ON 即 ∠ MO P ′ = ∠ NOQ 又 ∵ ∠ OQN = ∠ O P ′ M ∴ △ MO P ′ ∽ △ NOQ ∴ ON OM = NQ M P ′ = OQ O P ′ 在 ⊙ M 中,记其半径为 r ,则根据圆幂定理 得 OP ⋅ O P ′ = O M 2 − r 2 ,记为 a 又 OP ⋅ OQ = k ,记为 b ∴ b a ,得 OQ O P ′ = k O M 2 − r 2 ∵ OM , r , k 都为定值 ∴ OQ O P ′ 为定值 ∵ ON OM = NQ M P ′ = OQ O P ′ 又 ∵ OM , M P ′ 为定值 ∴ ON , NQ 为定值 又 ∵ OM 固定, ∠ MON = ∠ POQ 为定值 ∴ ON 固定 ∴ 点 Q 在以 N 为圆心, NQ 为半径的圆上运动(不经过点 O 的圆) 动图如下。
综上所述,反演变换的大多数题目都是由相似 解决的,有些甚至还用到了圆幂定理 ,可见反演变换套路之复杂。当然,以上列举的还仅仅时反演变换最基础的内容,不过即便这样也足以解决 90% 的初中反演类型的题目了,就如2025年广东省广州市越秀区一模卷的第25题第(3)小问 线生圆
读完这篇文章,你也应该差不多已经入门反演变换了,后续我还会出更多相关的内容,希望各位可以动动手指主动分享一下,扩大知识的传播面,让身边更多的人能够了解这些技巧。