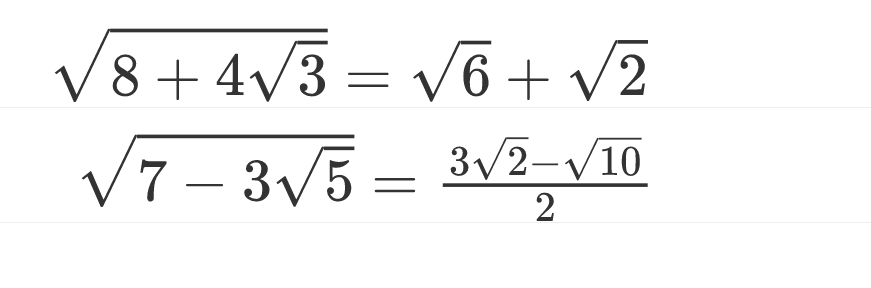这篇文章我会详细介绍初高中常见的双重根式化简问题,这尤其常见于三角函数计算中。
先来看可化简双重根式的一般形式:S=a±b
那么该式中如何去掉最外层的根号呢,或者说检验它可否被化简,以下我将运用待定系数法来讲解。
模型分析及证明#
首先观察原式,有 a,b 为正有理数,亦可知 S 化简后应为 m±n 的形式,且 m,n 为正有理数,那么我们可以令 m±n=a±b
等式两边同时平方即得 m+n±2mn=a±b
因为 m,n,a,b 都为正有理数,所以不妨令 {m+n=a,±2mn=±b (待定系数法)
化简即 {m+n=a,mn=4b
看到这样一个方程组,想必大家都很熟悉,这不就是韦达定理么。
所以下一步是构造一个关于 x 的一元二次方程,使 m,n 为其两根,则有 x2−ax+4b=0
其判别式为 Δ=(−a)2−4×1⋅4b=a2−b
则 x=2×1a±a2−b,得 m=2a+a2−b,n=2a−a2−b
因为 m,n 为正有理数,所以条件为判别式 Δ=a2−b 为可开尽方的有理数
最后即可得 a±b=2a+a2−b±2a−a2−b
例题精讲#
接下来我们看几道例题。
-
化简 8+43 .
解:由题,知Δ=82−42×3=16
∴原式=28+16+28−16=6+2
-
化简 7−35 .
解:由题,知Δ=72−32×5=4
∴原式=27+4−27−4=29−25=232−10
习题检验#
最后,给大家留几道习题。
- 判断 5+25 能否被化简:若能,则写出化简后的结果;若不能,请说明理由.
- 判断 37−127 能否被化简:若能,则写出化简后的结果;若不能,请说明理由.
- 已知 cosθ=532,运用公式 tan2θ=1+cosθ1−cosθ,计算 tan(90°−2θ) 的值.
习题的过程及答案将会另篇揭晓,留心关注哦~