写在前面#
首先我想对大家说一声抱歉哈,这篇文章我已经拖了非常非常久了,因为是中考题,所以其实我早就定稿这篇文章了,只是最近忙这些其他事情没来得及在博客上发布。今天好不容易有空,就想着先把这篇文章给补了。
这一道题是2025年的广州市中考真题,也因为我恰好就是2025届广州中考生,才更能体会这道题的含金量,于是考虑记录此篇。
在正式阅读本篇文章之前,建议提前学习双动线段比例最值问题——反演变换(2)。
真题再现#
以下2025年广州市中考第25题题面。
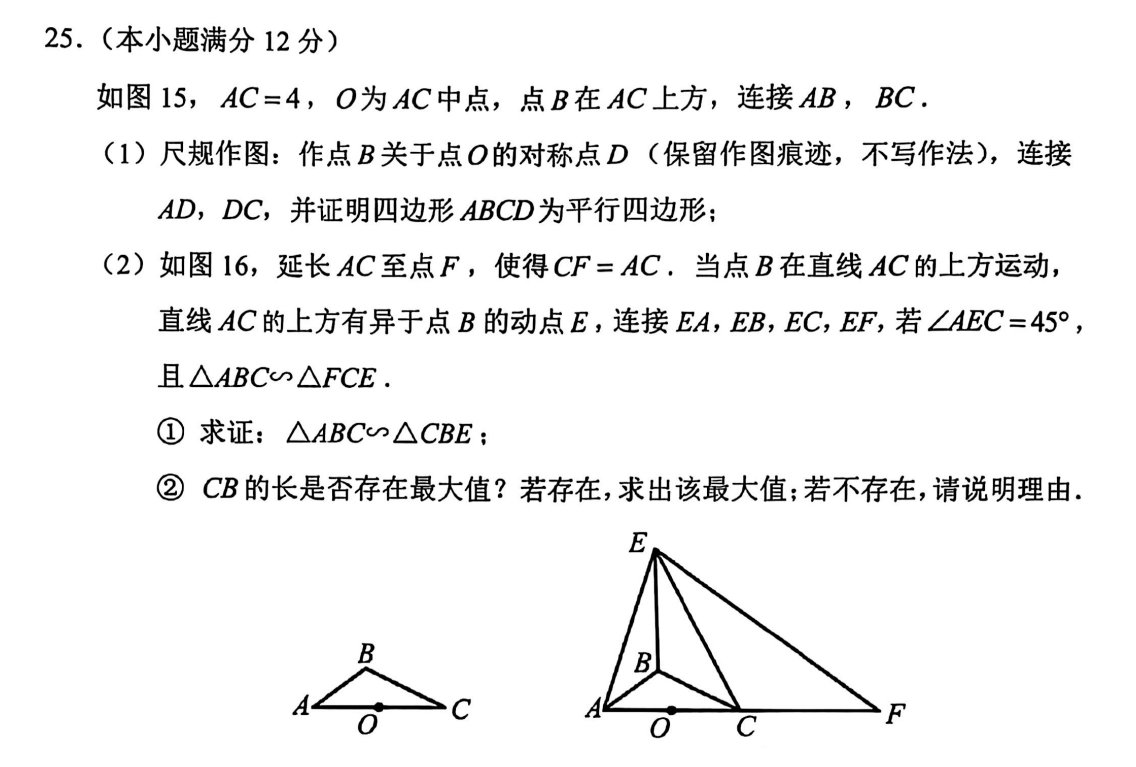
第(1)问太简单了,就是个尺规作图题,这里不做过多介绍了。
第(2)题第①小问#
其中第(2)问呢,又被分为两个小问①②,那我们就先来看第①小问:是一道证明题,要求我们证明两个三角形相似。既然是这样,那无非就是“两角”“两边夹一角”和“边边边”了,但是由于题目中已经给出了一对现成的相似三角形 △ABC∽△FCE,所以我们需要先把角导明白,毕竟能直接用角相等证明相似肯定比用边要方便很多。
那我们不妨设 ∠BAC=α,∠ACB=β,由题目中所给的相似,可得 ∠CFE=α,∠CEF=β,再由外角的性质,可得 ∠ACE=α+β,所以 ∠BCE=∠ACE−∠ACB=(α+β)−β=α,到了这时候,我们不难发现需要证明相似的两个三角形已经被推出一个角相等了,那这道题就算是完成 31 了,接下来该怎么做呢?
应该很容易发现,除了刚刚的 ∠BCE,我们无法进一步推导出其他 △CBE 中的角了,所以我们得换种思路,来看最开始提到的证明两个三角形相似的三种方法,其中“两角”和“边边边”都已经被排除了,所以将目光锁定在“两边夹一角”身上,目前我们所需要做的就是证明与这个角相邻的两条边与对应三角形的两条边分别成比例,(这句话可能有点长,我来用数学语言描述一下,即需要证明 CBAB=CEAC),如何呢?
还是题目所给的相似三角形,只需提取其中有关边的条件即可,即由 △ABC∽△FCE,得 CFAB=CEBC,将该比例等式进行变形,得到 CBAB=CECF。
诶?为什么我感觉我们所得到的比例式与需要证明的极其相似,但……还是不一样?
——原来是我们遗漏了一个重要条件!CF=AC!这样一来,我们即可通过“两边夹一角”证明这道题啦~
来看一下完整过程:
设∠BAC=α,∠ACB=β∵△ABC∽△FCE∴∠CFE=∠BAC=α,∠CEF=∠BCA=β∴∠ACE=∠F+∠CEF=α+β∴∠BCE=∠ACE−∠ACB=(α+β)−β=α∵△ABC∽△FCE∴CFAB=CEBC即CBAB=CECF又∵CF=AC∴CBAB=CEAC又∵∠BAC=∠BCE=α∴△ABC∽△CBE小结一下第①小问,整体上还是相对简单的,只需要我们打开思维,灵活且充分地运用题目条件即可证明。
第(2)题第②小问#
方法Ⅰ#
到了这一问,事情就开始复杂起来了。
这图形看市区的确是一线三等角模型,但是这似乎对我们解题并没有帮助,况且这类求动点运动轨迹的题目十分少见。
没办法,不是模型题,身处考场的我,只能开启思维迸发模式了——因为在开始做这一小问时,我只剩下10分钟左右的时间了。
我先从角的条件入手,企图可以直接求出点B的运动轨迹,但我很快发现,无论是从大题干给出的条件,还是上一小问所得的信息,都无法直接推出我想要的东西。此时已经过去了一两分钟了,在反复确认这个方法行不通后,我转变了新航道,把目光转移到“边”的身上,诶,还真就有新的发现!
因为需要利用边的条件,就只能从题目中所给出的相似三角形中推,而在第(2)问大题干中的一组相似 △ABC∽△FCE 就已经可以推出一个很关键的条件:CB=AC⋅EFCE,又因为 AC 是常量,所以 CB=EF4CE,到这里,整道题的解法就已经初见端倪了——一条动线段 CB 的长度被转化为另外两条共顶点动线段之比 EFCE 的倍数,是不是有点familiar(熟悉)的味道了呢?(参考双动线段比例最值问题——反演变换(2))
没错,到这一步这道题就基本上解决了,因为后面的步骤就是之前所讲的模型了!利用圆幂定理反A相似,即可顺利地将两个变量减少为一个,并且是建立在可以用已知运动轨迹的点 E 上求解的单线段最值问题。下面就直接看完整过程吧。

作△ACE的外接圆⊙M交EF于点N,连接AM,AN,MN,CM.∵△ABC∽△FCE∴CEBC=FEAC即ACBC=EFCE,BC=AC⋅EFCE=EF4CE在⊙M中,∠FAN=∠FEC又∵∠F=∠F∴△FAN∽△FEC∴EFAF=CEAN即EF4CE=AF4AN∵CF=AC=4∴AF=CF+AC=4+4=8∴EF4CE=84AN=2AN已知点N在⊙M上运动∴在△AMN中,AN≤AM+MN在⊙M中,∠AEC=45°∴∠AMC=2∠AEC=2×45°=90°又∵AM=CM∴∠MAC=45°∴在Rt△AMC中,cos45°=ACAM=22即AM=22AC=22×4=22∴MN=AM=22∴AN≤AM+MN=22+22=42即EF4CE=2AN≤22即CB≤22∴CB的最大值为22当然,以上还只是套用了模型的最初思路,虽然可以解出这道题,但还是有可以改进的点的:就如我们可以通过导角直接证明 △ABC∽△FNA,得到 ANBC=AFAC=21AN 一步到位,可以极大地简化了步骤,进一步节约时间。
只可惜我在考场上并没有写完过程😭(┬_┬)
方法Ⅱ#
鉴于官方做法为直接求出点 B 的运动轨迹,以及互联网上大部分的解题思路也是如此,这里也就简单提一下。
在前面讲方法Ⅰ的时候已经提到过,整个图形中并没有现成的与线段 CB 相关的定角来求出点 B 所在的轨迹圆(题目中没有说,但是这种情况下点 B 的轨迹大概率就是一个圆了,考场上可以任取几点观察,因为目前中考几何题目中的动点运动轨迹只能是直线或圆),所以轮到我们添辅助线了~
注意到整道大题的第(1)问要求的尺规作图~~(注意力惊人)~~,本质上是倍长中线!其实相当于给了我们一个小小的提示,那么在这一小问当中,也可以连接并倍长线段 BO 转化角的条件,最后其实是可以证明 ∠OBC=45° 的,定弦定角便可以确定点 B 的运动轨迹了!
请看完整过程。

延长BO至点H,使得OH=OB,作△OBC的外接圆⊙M,连接CH,OM,BM,CM.∵O为AC中点∴AO=CO∴在△AOB和△COH中,⎩⎨⎧AO=CO,∠AOB=∠COH,OB=OH∴△AOB≅△COH(SAS)∴AB=CH,∠BAO=∠HCO∵△ABC∽△CBE∴∠BAC=∠BCE∴∠HCO=∠BCE∴∠HCO+∠ACB=∠BCE+∠ACB即∠BCH=∠ECA∵△ABC∽△FCE∴CEBC=CFAB又∵CF=AC,AB=CH∴CEBC=ACCH∴△BCH∽△ECA∴∠CBH=∠CEA=45°即∠OBC=45°∴在⊙M中,∠OMC=2∠OBC=2×45°=90°∵OM=CM∴∠MOC=45°∴在Rt△OMC中,sin45°=OCCM=22∴CM=22OC=22×21AC=22×21×4=2∴BM=CM=2在△BCM中,CB≤CM+BM=2+2=22即CB的最大值为22
那么广州中考第25题的评估就结束啦~
我们也可以从中得到一些启发,像这样一道压轴题,出题人肯定是会给我们一些提示的(但不保证100%),以后做题应仔细观察题面(审题),充分利用题目所给的条件和其他默认已知信息,往往可以事半功倍!




